知识
阿尔法因子挖掘
一、传统与基础方法
1. 人工设计与金融理论
这是最经典的方法,依赖于研究员对市场的理解和金融学知识。
-
来源:基于成熟的金融理论或市场观察到的规律(异象)。
-
示例:
-
动量因子:过去赢家在未来继续赢,输家继续输。
-
价值因子:买入价格低于其内在价值的股票(如低市盈率P/E)。
-
规模因子:小市值公司股票表现优于大市值公司。
-
-
特点:逻辑清晰,可解释性极强,但难以发现新颖、复杂的因子。
2. 遗传编程
这是一种受生物进化论启发的自动化方法,也是早期自动化因子挖掘的主流技术。
-
过程:
-
初始化:随机生成一批因子表达式(初始种群)。
-
评估:计算每个因子的表现(如IC值)作为“适应度”。
-
选择:选择表现好的因子作为“父代”。
-
交叉与变异:父代通过交换部分表达式(交叉)或随机改变部分内容(变异)产生“子代”。
-
迭代:重复步骤2-4,直到因子表现不再提升或达到迭代次数。
-
-
特点:能自动生成公式化因子,但搜索空间巨大,效率低下,容易陷入局部最优。
二、现代机器学习方法
这类方法不生成可解释的公式,而是直接将数据输入复杂模型来预测收益,形成“非公式化阿尔法”。
1. 监督学习模型
-
树模型:如 XGBoost、LightGBM。能处理非线性关系,对特征工程要求相对较低,在量化领域非常流行。
-
神经网络:如 MLP(多层感知机)、LSTM(处理时间序列)、Transformer(捕捉截面关系)。模型容量大,能捕捉非常复杂的模式。
-
特点:预测能力可能很强,但本质是 “黑箱” ,难以理解其内在逻辑,存在信任问题和过拟合风险。
三、强化学习方法
这是目前最前沿的方向,将因子挖掘过程建模为一个序列决策问题,正如您阅读的论文《AlphaQCM》所做的那样。
-
核心思想:
-
状态:当前已生成的部分因子表达式。
-
动作:下一步要添加的运算符或特征。
-
奖励:一个完整因子表达式被评估后,其对现有因子池的协同贡献(如IC值的提升)。
-
-
主流算法:
-
Policy Gradient (e.g., PPO):如AlphaGen方法,直接学习一个策略函数来生成因子。
-
Distributional RL (e.g., IQN):如AlphaQCM方法,不仅学习期望收益,还学习收益的完整分布,能更好地处理不确定性,并利用估计的方差作为探索奖励,解决奖励稀疏和非平稳性问题。
-
-
特点:
-
优点:能够生成协同的、公式化的阿尔法集合,兼顾了可解释性和自动化挖掘能力。
-
挑战:对建模和算法要求高,需要处理非平稳性和奖励稀疏等核心难题。
-
四、自动化机器学习
-
理念:将整个因子挖掘流程(包括特征工程、模型选择、超参数调优等)全面自动化。
-
示例:AlphaEvolve 框架,利用AutoML-Zero的思想,从零开始进化出完整的机器学习流水线来预测收益。
-
特点:自动化程度最高,但生成的结果可能极其复杂,可解释性最差。
滚动窗口-最优投资组合
指数平滑法vs滚动窗口法
时间序列模型和滚动窗口
场景一:金融预测(例如预测股价波动率)
-
底层模型: GARCH模型(一个经典的时间序列模型,用于刻画波动率的聚集性)。
-
应用方法: 滚动窗口。
-
过程:
-
选择窗口长度,比如3年(756个交易日)。
-
用第1天到第756天的数据拟合GARCH模型,预测第757天的波动率。
-
将窗口向前滚动一天,用第2天到第757天的数据重新拟合GARCH模型,预测第758天的波动率。
-
不断重复此过程。
-
-
在这里的联系:
-
时间序列模型 (GARCH) 提供了预测波动率的能力。
-
滚动窗口 确保了这种能力是与时俱进的,它让模型参数根据最近3年的市场状况不断更新,从而产生更稳健、更可靠的样本外预测。
-
场景二:投资组合优化(您上一个问题中的主题)
-
底层模型: 可能不是一个复杂的预测模型,而是一个优化器(如马科维茨均值-方差模型),它需要输入资产的预期收益率和协方差矩阵。
-
应用方法: 滚动窗口。
-
过程:
-
用过去5年的历史数据(窗口)计算资产的 historical returns 和 covariance matrix。
-
将这些估计值输入优化器,得到最优资产权重。
-
持有这个组合一段时间(例如一个月)。
-
将窗口向前滚动一个月,用新的5年数据重新计算预期收益和协方差,重新优化得到新的权重。
-
-
在这里的联系:
- 滚动窗口在这里用于更新优化模型的输入参数。它本质上是在创建一个动态的、自适应的时间序列模型,这个模型的输出是资产权重。权重序列本身就是一个时间序列。
场景三:模型验证与回测
这是滚动窗口最核心的用途之一。无论你的时间序列模型多复杂,要评估它的真实性能,必须使用滚动窗口(或扩展窗口)进行回测,以防止“前视偏差”。这体现了滚动窗口作为评估框架的角色。
基于价值和基于策略
| 特征 | 基于价值 | 基于策略 |
|---|---|---|
| 它学习什么? | 价值函数 - 一个状态或状态-动作对有多好。 | 策略本身 - 一个从状态到动作的映射。 |
| 它输出什么? | 一个价值表或价值函数 Q(s, a) 或 V(s)。 |
一个策略 π(a|s),通常是一个概率分布。 |
| 如何做决策? | 间接的。比较所有动作的价值,然后选择价值最高的那个(例如,贪婪策略)。 | 直接的。根据学习到的策略 π 直接采样一个动作。 |
| 动作空间 | 适用于离散的、低维的动作空间。当动作空间连续或很大时,比较所有 Q(s, a) 会非常困难。 |
适用于连续的、高维的动作空间(如机器人控制)。可以直接输出一个连续的动作值。 |
| 策略的类型 | 通常学习的是确定性策略(总是选择最好的动作)。 | 可以轻松学习随机性策略,这对于探索和环境本身具有随机性的情况非常有用。 |
| 收敛性 | 通常更容易收敛和分析。 | 可能收敛到局部最优,训练过程可能不太稳定。 |
| 典型算法 | Q-Learning, DQN, SARSA | REINFORCE, PPO, TRPO |
投资组合优化VS交易策略优化
| 维度 | 投资组合优化 | 交易策略优化 |
|---|---|---|
| 1. 核心问题 | “买什么?” 以及 “买多少?” | “何时买?” 以及 “何时卖?” |
| 2. 优化目标 | 在特定风险水平下最大化收益,或为特定收益目标最小化风险。关注静态的资产配置。 | 最大化单次或多次交易的盈利性(如夏普比率、累计回报)。关注动态的择时。 |
| 3. 时间尺度 | 中长期(周、月、季度、年)。调整频率较低。 | 中短期(秒、分钟、小时、日)。交易频率较高。 |
| 4. 主要输入 | • 资产的预期收益率 • 资产的波动率(风险) • 资产间的相关性/协方差矩阵 • 投资约束(如预算、行业限制) |
• 价格/量 技术指标(均线、RSI等) • 基本面 数据(财报、新闻) • 市场微观结构 数据(订单簿) • 交易成本(佣金、滑价) |
| 5. 输出结果 | 一组资产权重(例如:60%股票,30%债券,10%黄金)。这是一个比例。 | 具体的交易信号(买入/卖出/持有)和头寸大小。这是一个动作指令。 |
| 情况一:分层强化学习架构 | ||
| 你可以使用相同的算法(如PPO),但在不同层级: |
- 顶层(组合优化):PPO学习战略资产配置,动作是权重调整
- 底层(交易优化):PPO学习战术执行,动作是具体的买卖指令
情况二:端到端的统一框架
如果你的动作空间设计得足够巧妙,一个RL智能体可以同时学习两者:
动作 = [配置权重, 择时信号, 风险控制参数]
但这需要极其复杂的状态空间和奖励函数设计。
收缩协方差矩阵
核心思想:在“过拟合”和“无用”之间找到最佳平衡
收缩协方差矩阵的根本目的,是为了得到一个更稳定、更准确的真实协方差矩阵估计值。
要理解它,我们首先需要明白传统方法的问题。
1. 传统样本协方差矩阵的问题
当我们有N个资产(比如1000只股票),通常用历史收益率数据来计算样本协方差矩阵。
-
问题一:数据不足,噪音太多
- 假设我们有3年(约750天)的数据去估计1000只股票的协方差矩阵。我们需要估计的参数非常多(协方差矩阵中有
N*(N-1)/2个独特的协方差和N个方差)。 - 相对较少的观测值去估计大量的参数,会导致估计结果充满抽样误差(也就是“噪音”)。这个矩阵捕捉到的很多“规律”,其实是数据中的随机波动,而非资产间的真实关联。
- 假设我们有3年(约750天)的数据去估计1000只股票的协方差矩阵。我们需要估计的参数非常多(协方差矩阵中有
-
问题二:数值不稳定,导致优化器“发疯”
- 在投资组合优化中(比如马科维茨模型),我们需要使用协方差矩阵的逆矩阵。
- 一个充满噪音的、病态的样本协方差矩阵,其逆矩阵会非常不稳定。这会导致优化器给出一些看似收益极高但实际荒谬无比的权重(比如给某些资产配置1000%的权重,做空另一部分900%),这些权重对输入数据的微小变化极其敏感,在实践中完全无法使用。
2. 收缩的解决方案:妥协的智慧
“收缩”是一种妥协策略,它承认样本协方差矩阵有缺点,但并非一无是处。它的核心思想是:
将“不稳定的但可能包含细节的样本协方差矩阵”与“一个非常稳定的但过于简化的目标矩阵”进行加权平均。
这个过程的公式非常简单:
收缩后的协方差矩阵 = λ * 目标矩阵 + (1 - λ) * 样本协方差矩阵
这里的 λ (Lambda) 是一个介于0和1之间的数,被称为收缩强度。
现在我们来分解这个公式的关键部分:
a) 样本协方差矩阵
- 优点: 无偏,理论上包含了所有资产关系的真实信息。
- 缺点: 高方差,不稳定,噪音多。
b) 目标矩阵
- 作用: 作为一个稳定器。它是一个结构极其简单、估计误差极小的模型。
- 常见选择:
- 单因子模型:比如市场模型(所有股票的联动都只通过一个共同因素——市场指数来解释)。
- 常数相关矩阵:假设所有资产两两之间的相关性都是同一个常数(比如所有资产对的平均历史相关性)。
- 对角线矩阵:只保留样本矩阵对角线上的方差,而将所有非对角线上的协方差(即相关性)设为零。
- 优点: 极其稳定,方差极低。
- 缺点: 偏差很大,因为它是对现实世界过于简化的描述。
c) 收缩强度 (λ)
- 这是一个调节旋钮。
- 如果 λ = 0:结果就是原始的样本协方差矩阵。我们完全信任数据,承担所有不稳定的风险。
- 如果 λ = 1:结果就是目标矩阵。我们完全抛弃数据中的具体信息,得到一个极其稳定但可能忽略了很多真实结构的模型。
- 最优的 λ:通过统计方法(如Ledoit-Wolf定理)计算得出,旨在最小化估计的总体误差(偏差² + 方差)。通常,资产数量越多、历史数据越短,最优的 λ 就越大。
一个生动的比喻
想象你要预测明天的天气:
- 样本协方差矩阵 就像是一个复杂的局部气候模型。它非常精细,考虑了本地的风速、湿度、云量等所有细节(好比所有资产两两之间的关系)。但如果输入数据有微小误差,它的预测结果可能会天差地别(不稳定)。
- 目标矩阵 就像是 “明天天气和今天一样” 这种简单至极的预测。它非常稳定,不会瞎猜,但显然忽略了天气变化的动态(偏差大)。
- 收缩协方差矩阵 就像是将这两个预测结合起来。
- 你最终采用的预测 = λ * “明天和今天一样” + (1 - λ) * “复杂模型的预测”。
- 如果复杂模型本身很不稳定(数据量少),你就会更相信简单的预测(λ 较大)。
- 如果复杂模型基于海量数据,非常可靠,你就会更相信它(λ 较小)。
通过这种“收缩”,你得到了一个既比简单预测更准确,又比复杂模型更稳定的、鲁棒性极强的最终结果。
在投资组合优化中的意义
使用收缩后的协方差矩阵,可以:
- 极大地提升优化结果的稳定性:投资组合权重不会因为历史数据窗口的微小滚动而发生剧烈变化。
- 产生更合理的资产配置:避免出现极端权重(巨量做多或做空),使组合权重更分散,更符合常识。
- 提高样本外表现:由于减少了过拟合(拟合了历史数据中的噪音),基于收缩矩阵构建的投资组合在未来(样本外)的表现通常会更好、更可靠。
总结来说,收缩协方差矩阵是一种通过引入一点有偏但稳定的信息,来大幅降低估计误差的统计技术,是量化投资中处理高维数据、提升模型稳健性的核心手段之一。
强化学习算法
【用游戏揭秘人工智能原理(4)— 时序差分算法TD】 https://www.bilibili.com/video/BV1La411i7zy/?share_source=copy_web&vd_source=7e6ea0697121b5af3f41d4244e06fb27
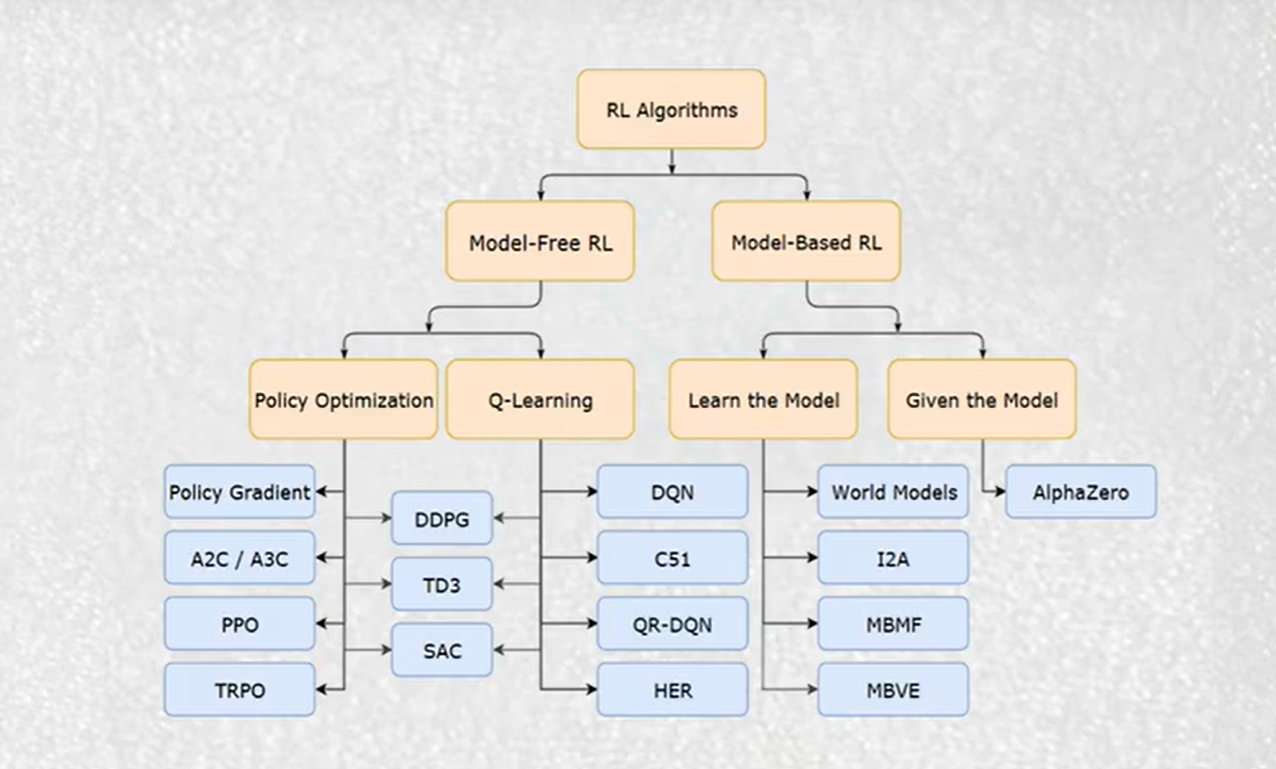
1.马尔科夫链
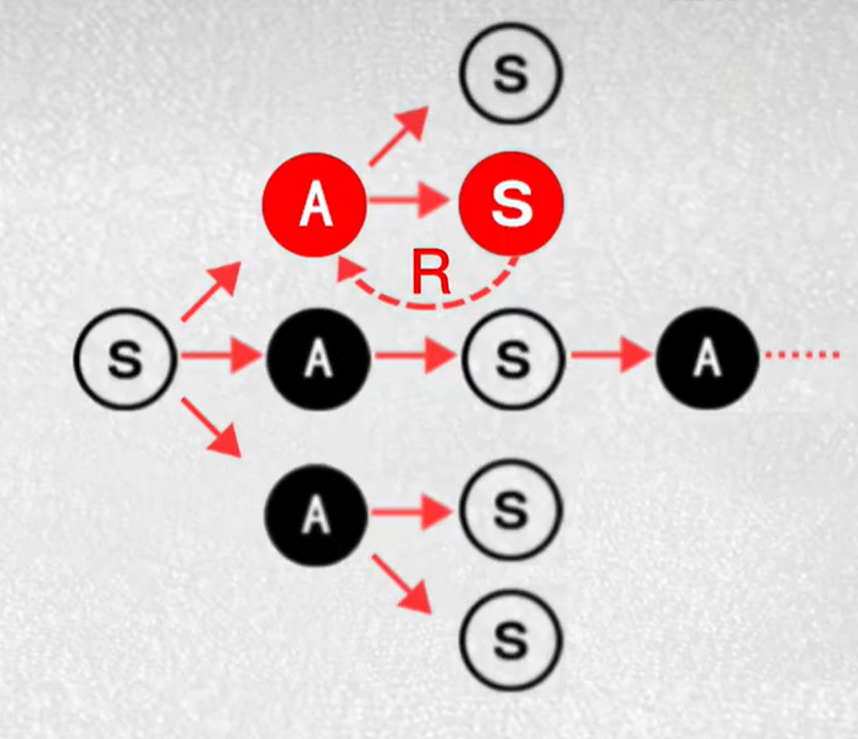
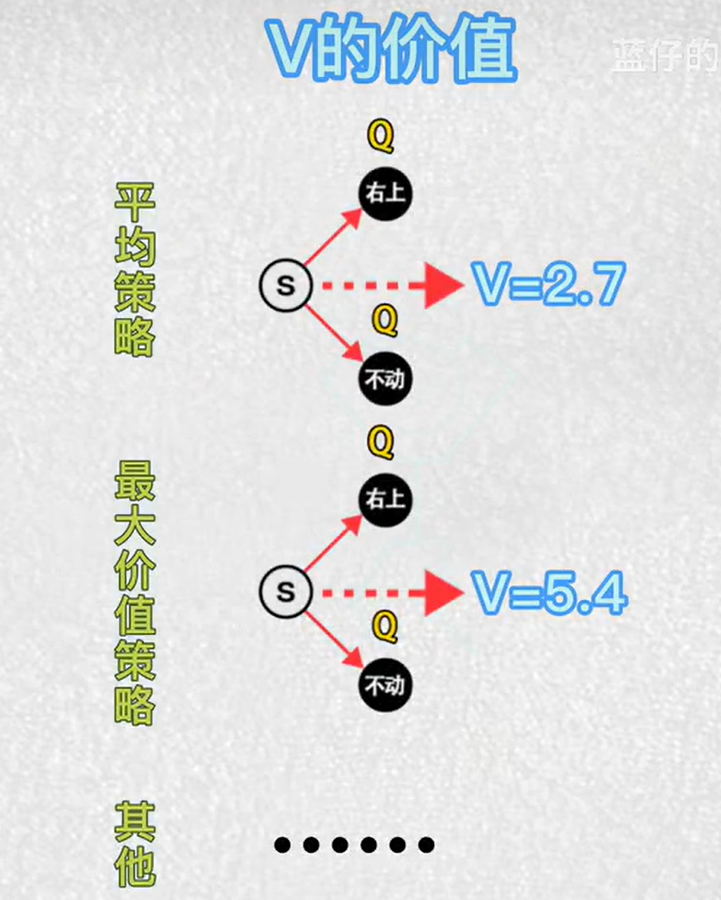
2.强化学习中Q和V的概念
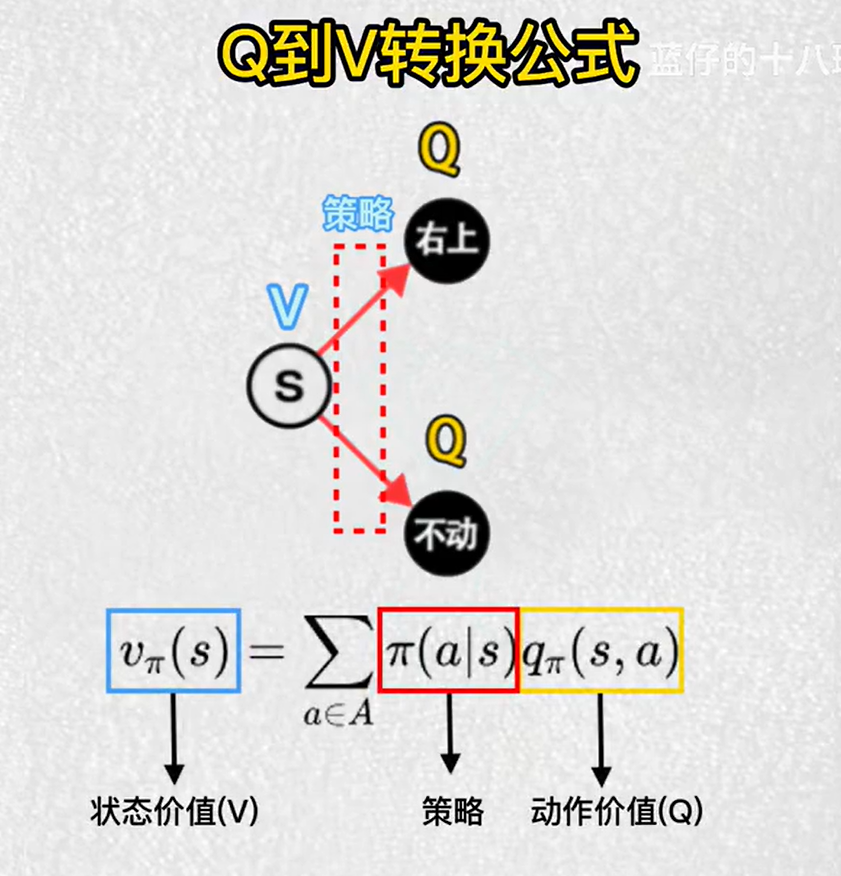
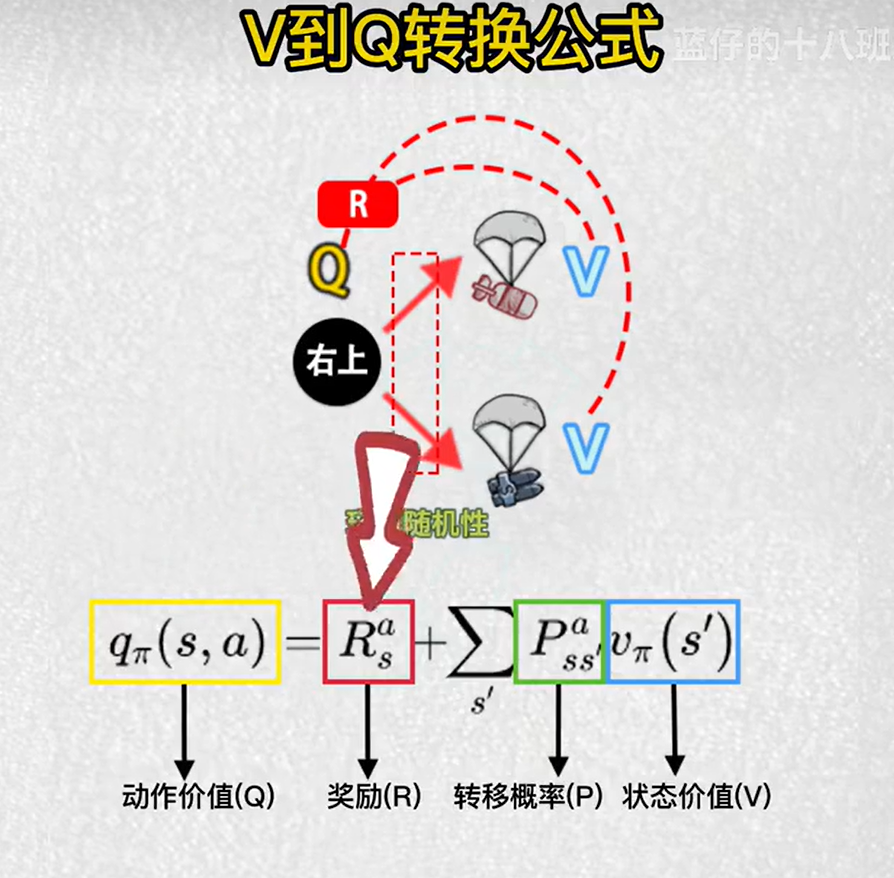
3.蒙特卡罗法
每一局奖励累加来更新状态
游戏结束后逐步向前累加来计算各个节点的价值
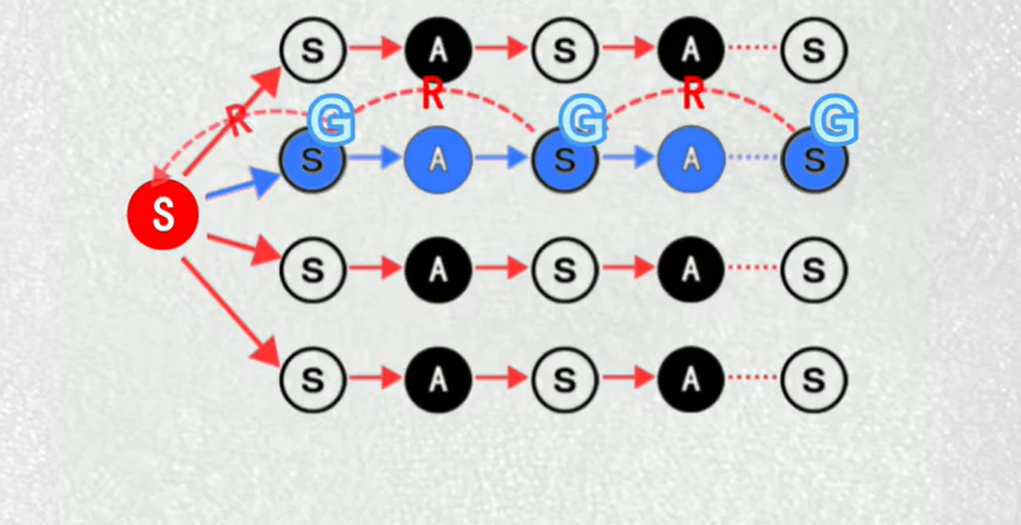
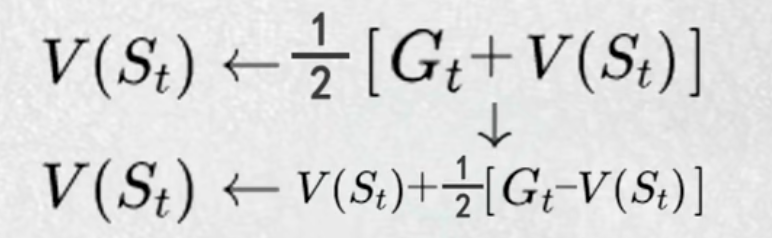

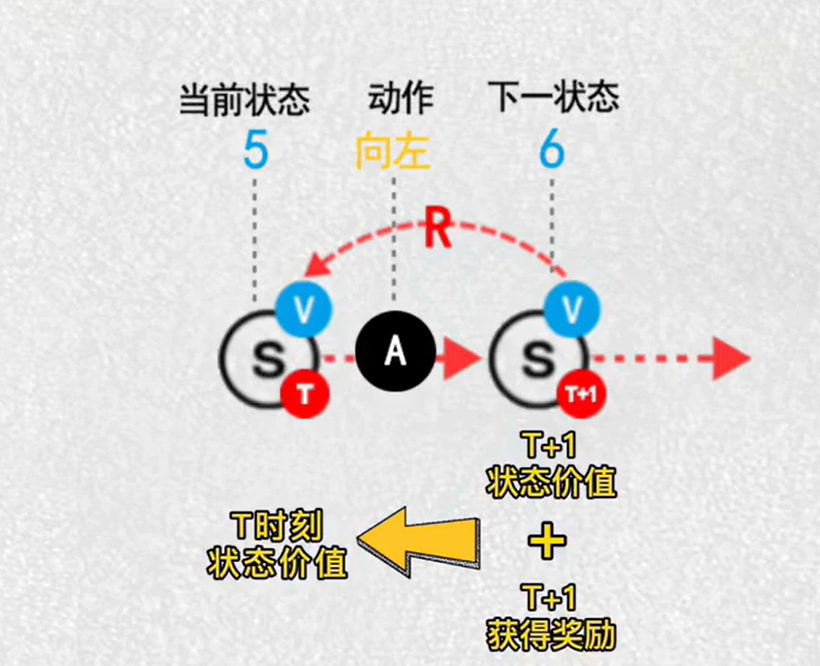
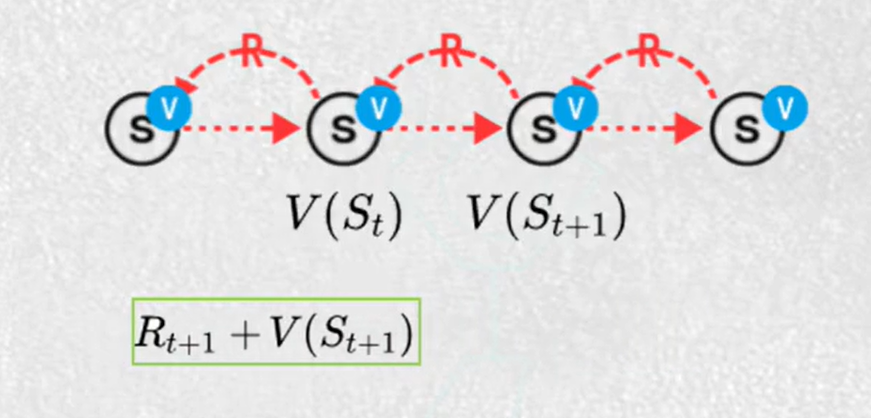
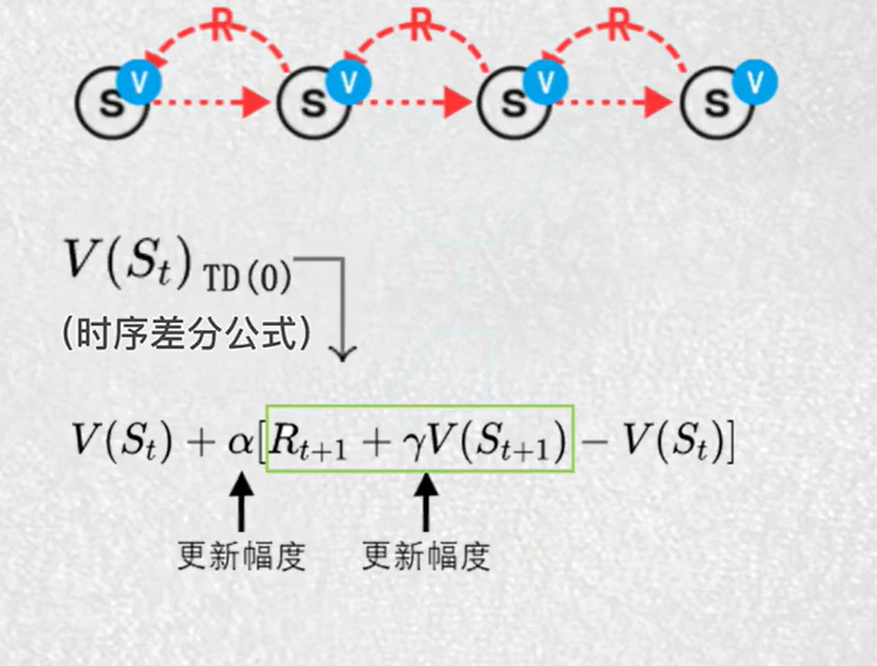
4.时序差分算法TD
每一步都更新
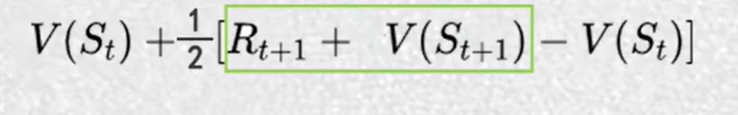
5.Qlearning(上),Qlearning的想法


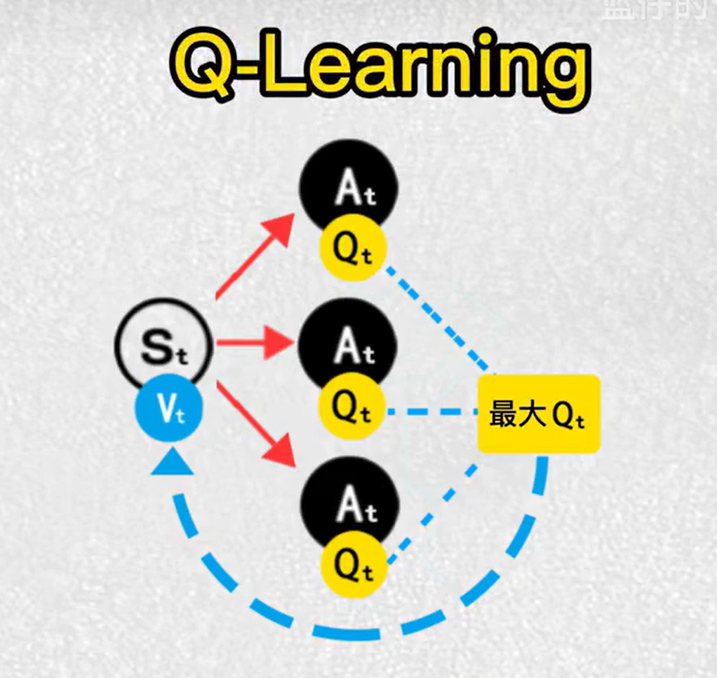
6.Q-Learning 值函数
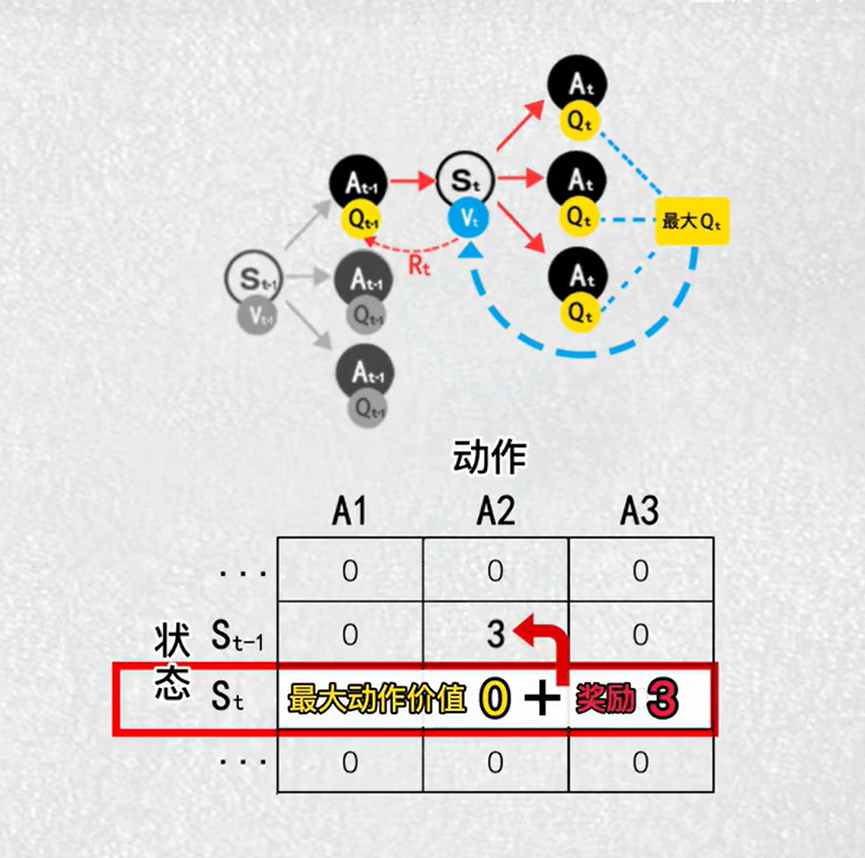
目的:找到最大价值的动作
算法:选择动作最大的价值,作为V的更新目标
用计算出来的价值推算出动作的价值
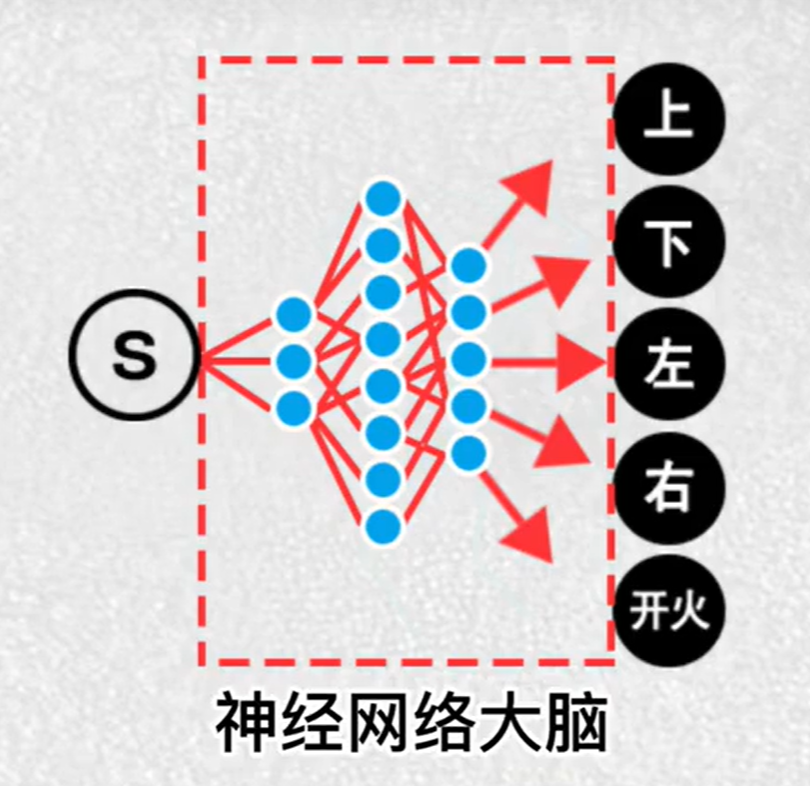
7.策略梯度
让神经网络大脑不断的寻找对的动作
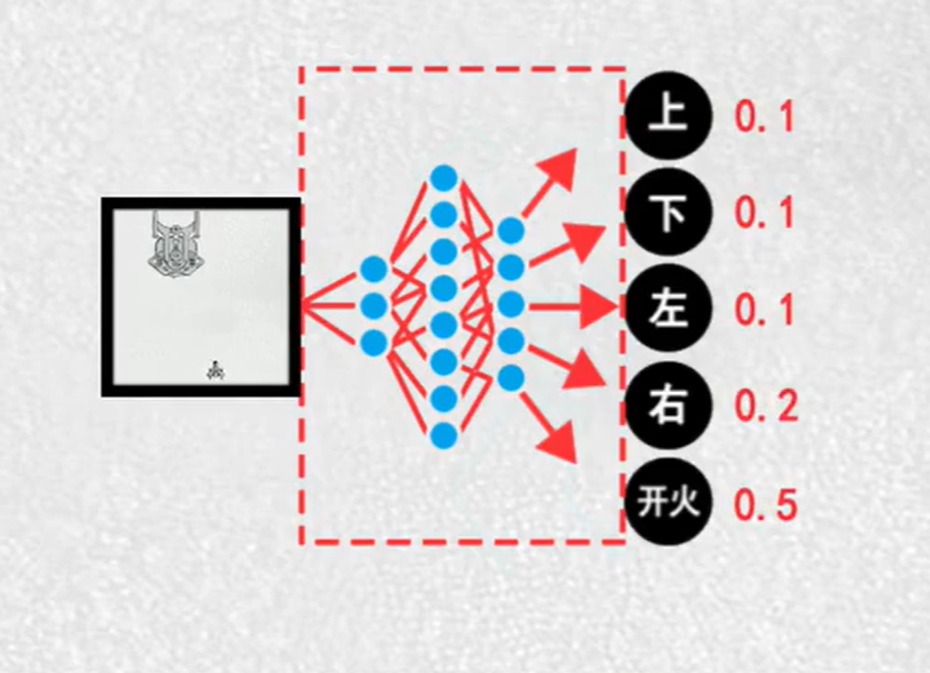
AI看到:每一帧动作画面
要做:每一帧的动作分布
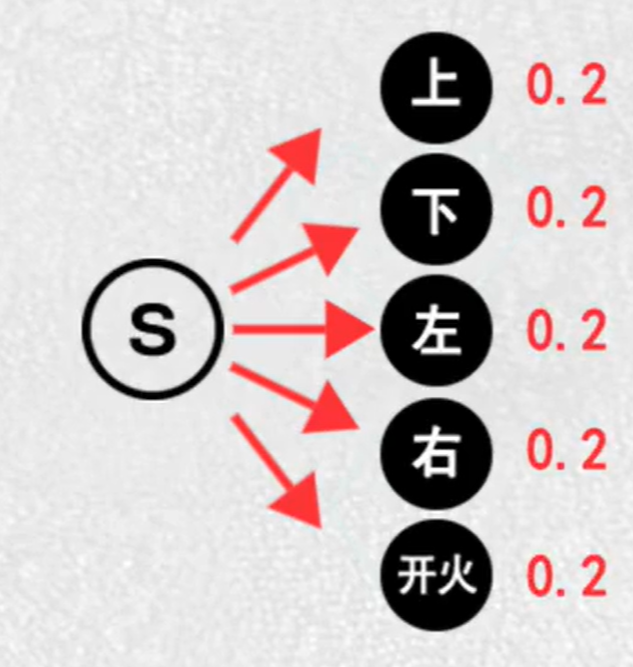
起初:AI只能随机选择动作
蒙特卡洛法:计算每一状态帧下的累计奖励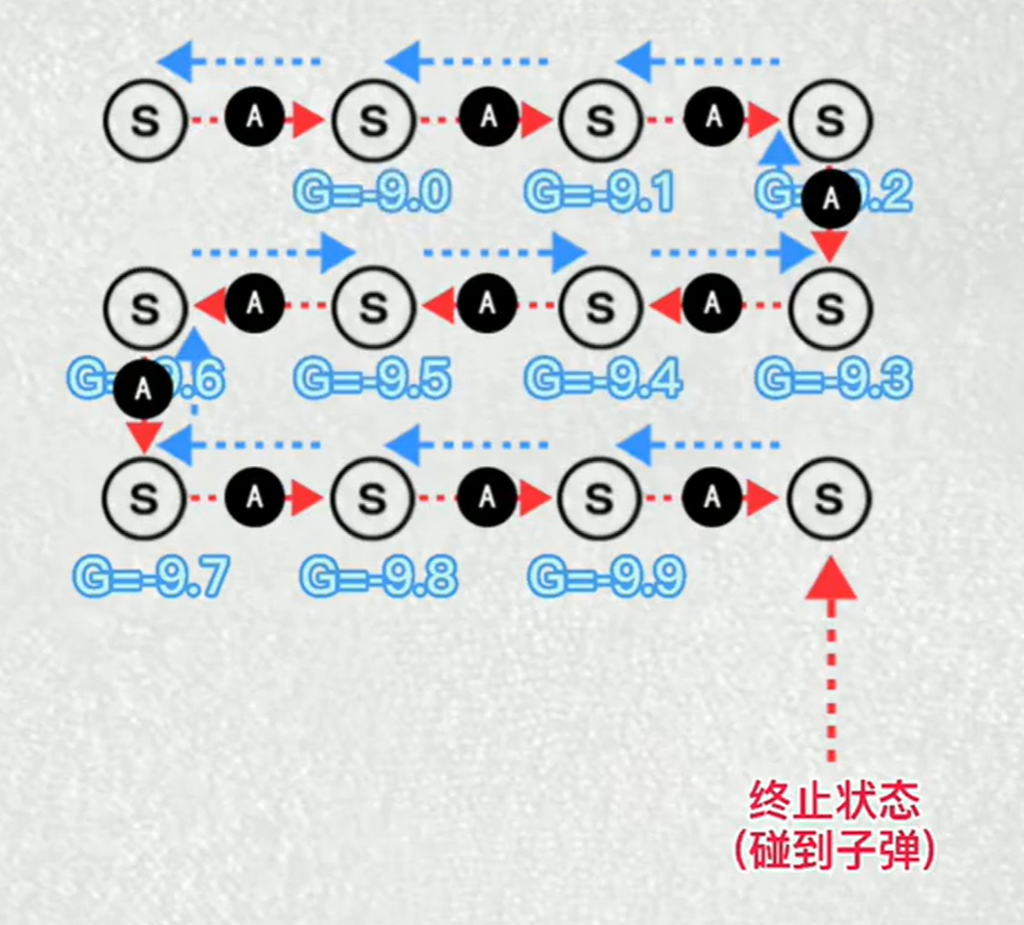
如果奖励是正数,朝着正确动作更新,累计奖励越多,更新的幅度越大
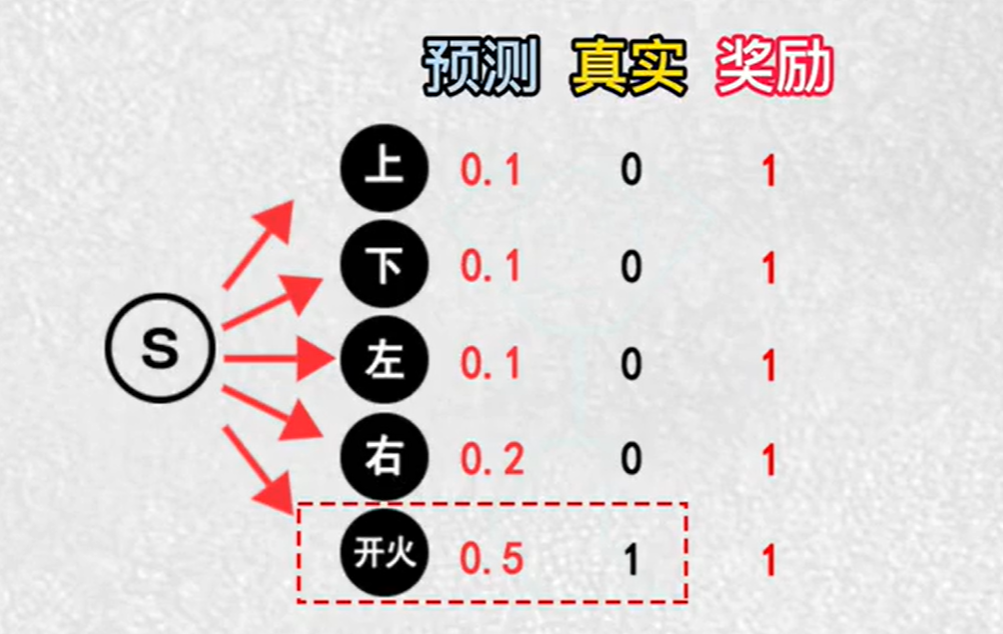
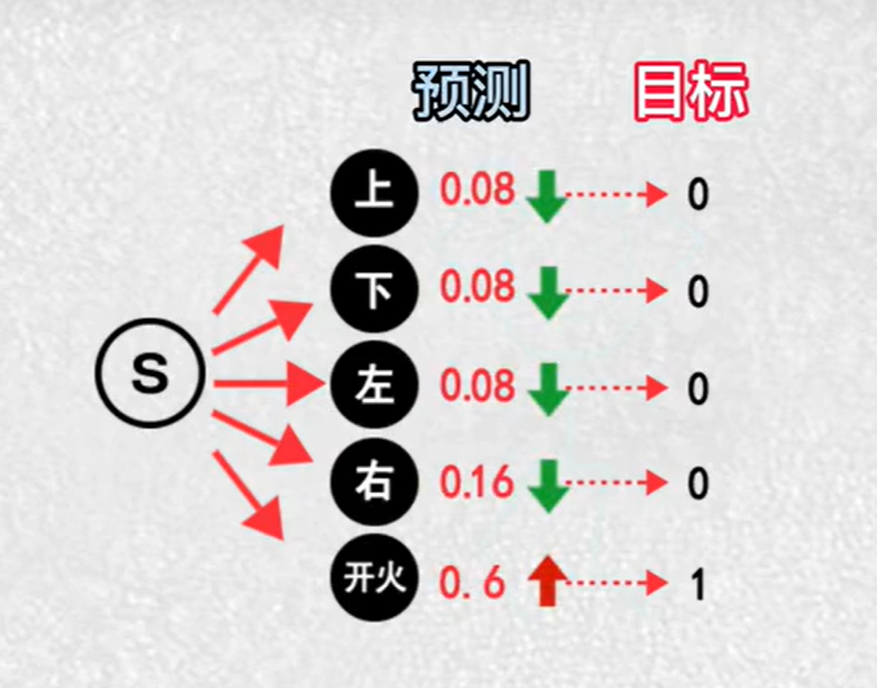
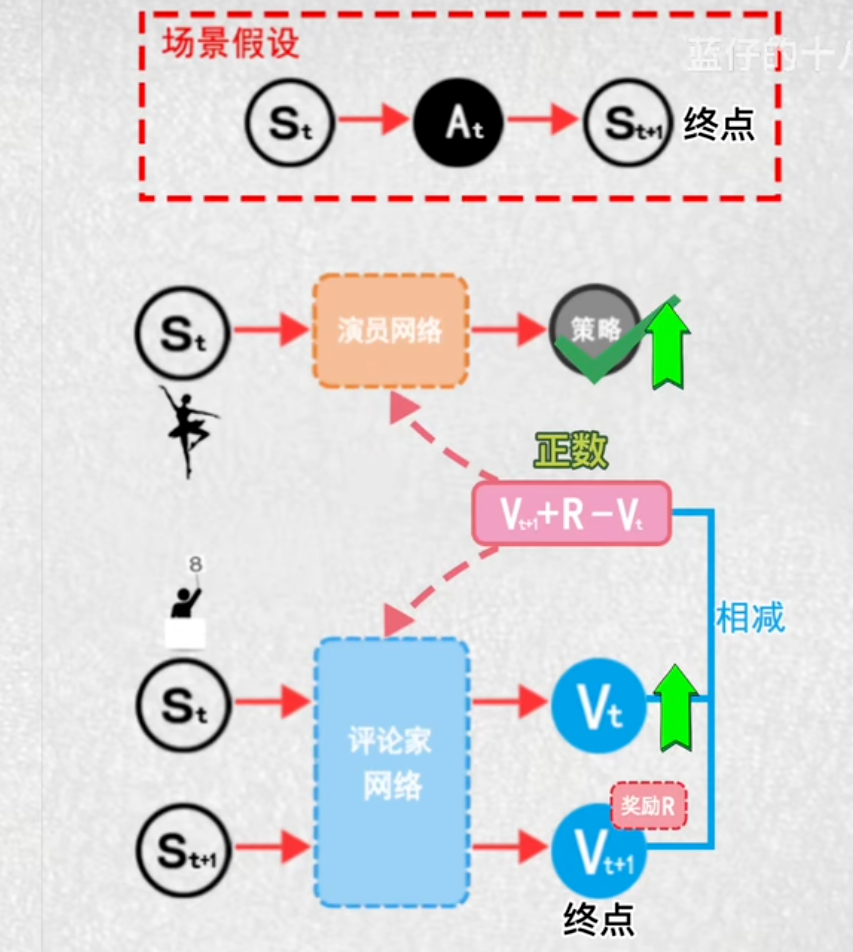
8.演员评论家算法
演员大脑:根据当前各个状态,输出主角各个动作的概率
评论家大脑:给演员的动作打分,高分——演员提高此动作输出概率
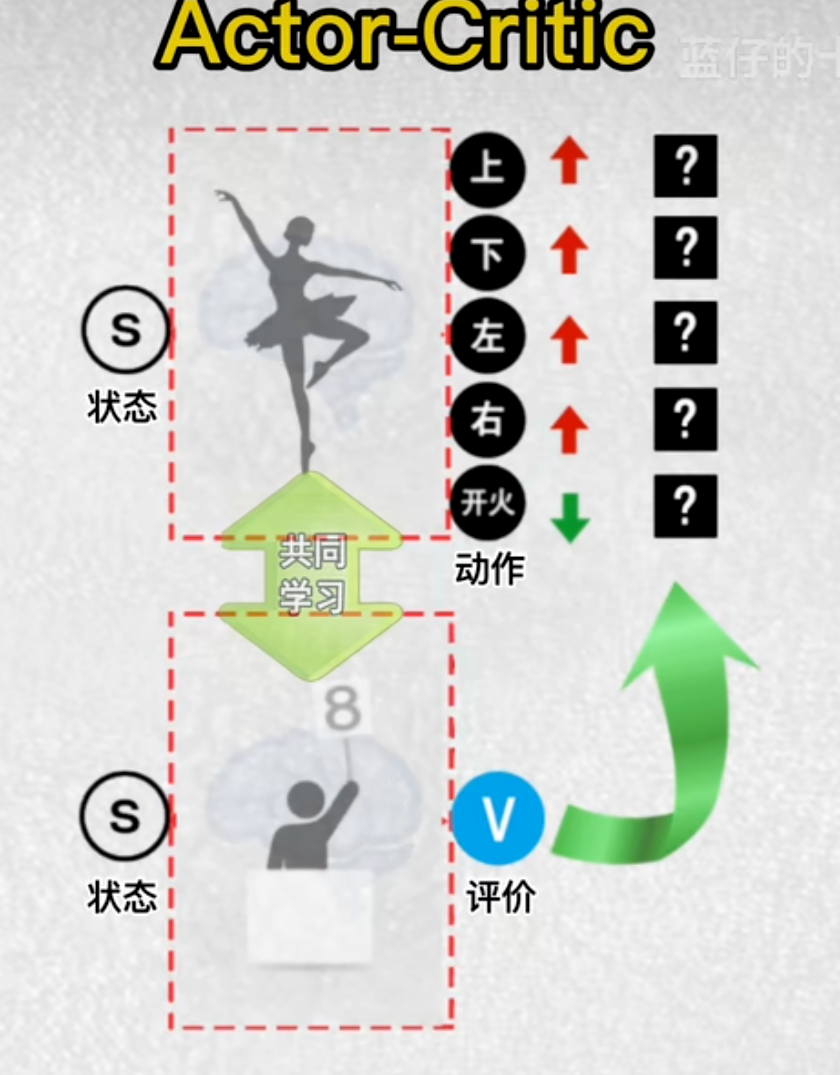
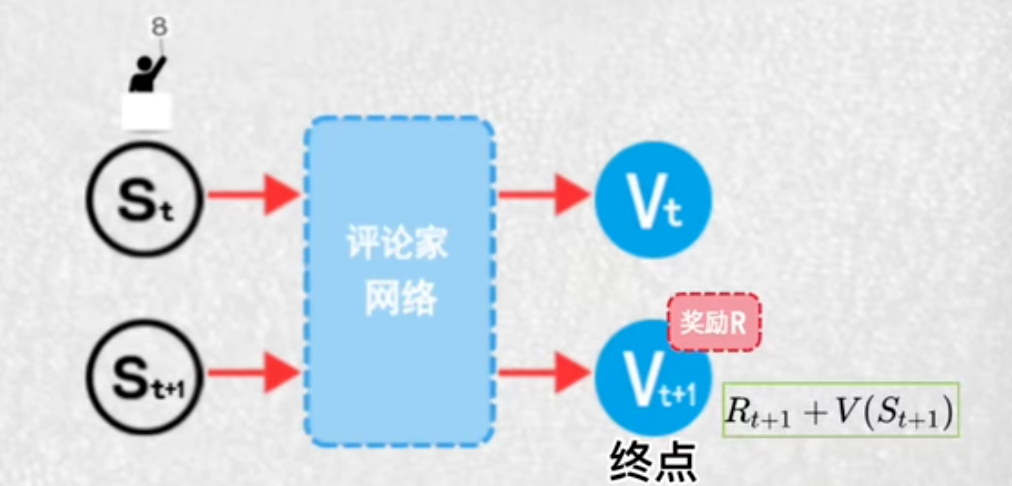
演员在t时刻通过其神经网络,输出动作概率,并选择一个动作后来到t+1时刻
评论家分别计算这两个状态的价值
把t+1看作是动作的终止,奖励累加方式,计算t时刻最新的状态价值,再相减,如果差值是正数,评论家就将当前状态价值,朝着价值高的方向更新
演员:得分高,提高这个动作的输出概率
9.DQN(deep-Q-learning)
将原来的表格换成神经网络
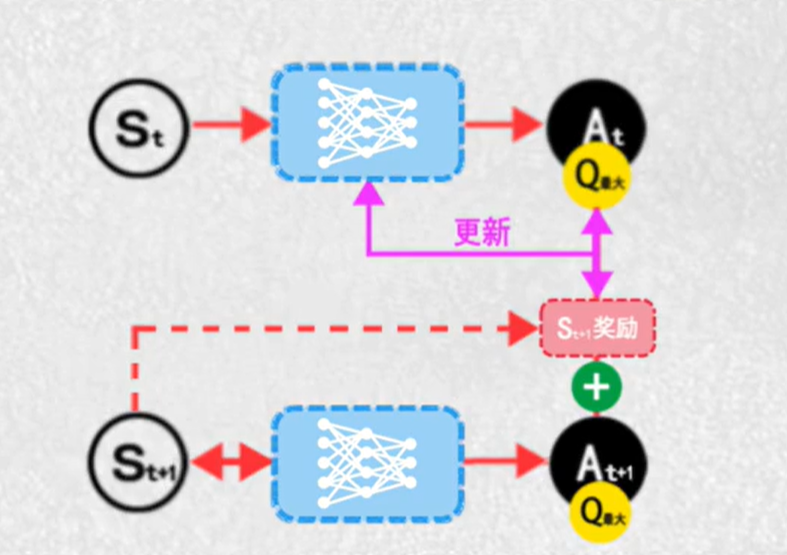
函数能连续表达连续的状态价值和动作价值的关系
神经网络拟合函数

10.AI玩功夫(上)-强化学习案例
11.AI玩功夫(下)-强化学习案例
生成订单簿数据
LOB 就是“限价订单簿”。
您可以把它想象成一个电子化的、实时的、不断变化的“愿望清单”,上面记录了市场上所有买家和小卖家对于某一只股票(或任何金融资产)在当前时刻的所有买卖意向。
想象一下您要买一套房子:
- 买家们会说出他们愿意出的最高价格(比如:“我最高出300万”,“我最高出295万”)。
- 卖家们会说出他们愿意接受的最低价格(比如:“我至少卖310万”,“我至少卖315万”)。
如果把所有这些买家和卖家的出价都收集起来,按价格从高到低(买家)和从低到高(卖家)排列,就形成了一个“房产订单簿”。
金融市场上的LOB就是这个原理,只不过它完全电子化、自动化,并且每秒变化成千上万次。
LOB的核心结构
一个典型的限价订单簿有两边:
-
买方(Bid):想买的人。他们报出自己愿意支付的最高价格。
- 特点:价格越低越好(对他们而言)。所以买方的报价从高到低排列。最高的买价叫做 “最佳买价”。
-
卖方(Ask 或 Offer):想卖的人。他们报出自己愿意接受的最低价格。
- 特点:价格越高越好(对他们而言)。所以卖方的报价从低到高排列。最低的卖价叫做 “最佳卖价”。
关键概念:
-
买卖价差:最佳卖价 减去 最佳买价。这是市场上最核心的指标之一。
-
比如:最佳买价是
$100,最佳卖价是$100.01,价差就是$0.01。 -
价差越小,说明市场流动性越好,交易越活跃。
-
-
深度:在每个价格点上,有多少股(或手)的订单在排队。
- 比如:在
$100的买价上,有500股在排队;在$100.01的卖价上,有300股在排队。这显示了市场在当前位置的“厚度”或承压能力。
- 比如:在
LOB里会发生什么“事件”?
订单簿不是静态的,它会随着以下事件动态变化:
-
提交新限价单:一个新的买卖意向加入队列排队。
-
撤单:排队中的订单被取消。
-
市价单:不指定价格,直接按照当前最好的价格成交。这会立刻消耗掉队列一方的订单。
限价订单(图2)指定了一个价格,对于买单(买价)不得超过该价格,对于卖单(卖价)不得低于该价格。限价订单在LOB的相应侧以挂单形式排队。
市价订单则表示交易者愿意立即接受当前可得到的最佳价格。
在实时交易中,向市场注入订单会引发其他市场参与者的活动,这通常会将价格推离该交易者的方向。这种活动被称为市场影响。